KAN

现在我们有了 KAN 的原型，其计算图完全由方程式(2.1)指定，并在下图(b)中进行了说明

1. 输入维度为 2，呈现为一个两层神经网络
2. 激活函数放置在边edges上而不是节点nodes上(节点上执行简单求和)，中间层的宽度为2n+ 1

对于一个光滑 $f:[0,1{]}^n\to R$，如下所示(定义为公式2.1)

$f(x)=f(x_1,\cdots ,x_n)=\sum _{q=1}^{2n+1}{\mathrm{\Phi }}_q(\sum _{p=1}^n{\varphi }_{q,p}(x_p))$

1. 由于论文中没有细致指出每一个变量的含义，但考虑到本文追求的详尽、细致的缘故，故我补充解释一下，其中各个变量的含义
   其中，$x_p$即代表向量$x$的第$p$个元素，故$p$的范围是从$1$到$n$($n$是输入向量的维度)
   $q$ 这个索引用于遍历外部函数 $\mathrm{\Phi }$ 的每个组成部分
   故有一元函数${\varphi }_{q,p}$(或称单变量函数)处理输入向量$𝑥$的第$p$个分量，并为第$q$个外部函数的求和贡献一个项

   定理指出，你可以用 2n+1 个这样的外部函数——每个外部函数 ${\mathrm{\Phi }}_q$ 是一个一元函数(它作用于由内部一元函数${\varphi }_{q,p}$的输出组成的求和)，来表示任何多变量函数 $f$

2. 总之，每个函数都可以用一元函数和求和来表示(since every other function can be written using univariate functions and sum)，看似前途一片光明，因为学习高维函数可以因此归结为学习多项式数量的一维函数(learning a high-dimensional function boils down to learning a polynomial number of 1D functions)
   然而，这些一维函数可能是非光滑甚至是分形的，因此在实践中可能无法学习(However, these 1D functions can be non-smooth and even fractal, so they may not be learnable in practice)

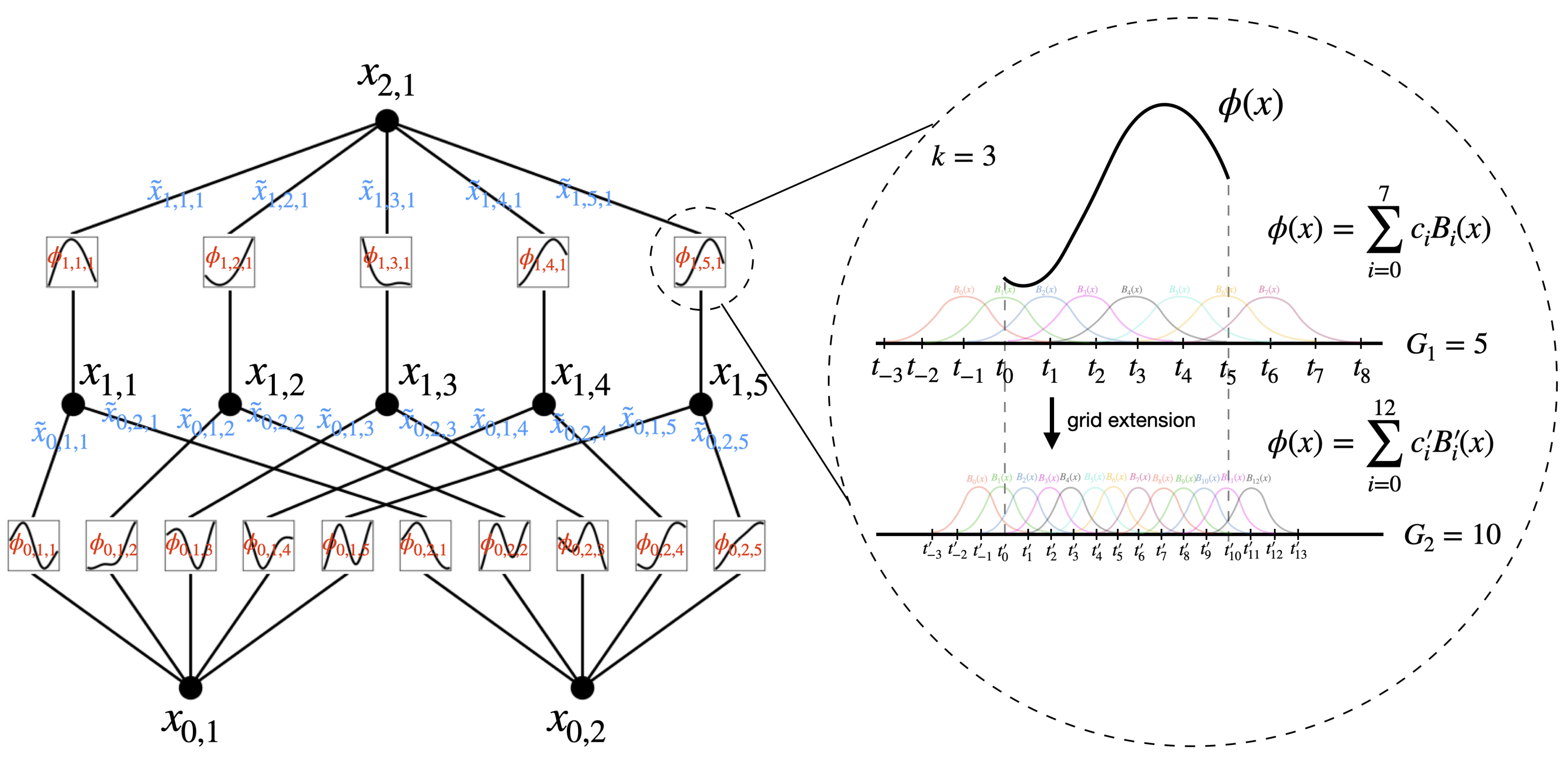
原方案

在MLPs中，一旦我们定义了一个层(由线性变换和非线性组成)，便可以堆叠更多层使网络更深

类似的，要构建深层KANs，首先要回答：“什么是KAN层？” 原来，具有输入维度和输出维度的KAN层可以被定义为一维函数矩阵(定义为公式2.2)

其中函数ϕq,p𝜙𝑞,𝑝具有可训练参数

1. 在Kolmogorov-Arnold定理中，先“散”后“聚”
   内部函数 ${\varphi }_{q,p}$ 形成一个KAN层，其中输入维度 $n_{in}=n$，输出维度 $n_{out}=2n+1$
   这表明每个输入变量$x_p$通过一组函数转换，输出的数量是输入数量的两倍加一，这样设计是为了充分捕获输入特征的信息并转化为中间表示
   外部函数{\Phi_q}形成一个KAN层，其中输入维度 $n_{in}=2n+1$，输出维度 $n_{out}=1$
   这层的功能是将内部函数层的所有输出整合起来，形成最终的模型输出

   因此，方程2.1中的Kolmogorov-Arnold表示简单地由两个KAN层组成
   $f(x)=f(x_1,\cdots ,x_n)=\sum _{q=1}^{2n+1}{\mathrm{\Phi }}_q(\sum _{p=1}^n{\varphi }_{q,p}(x_p))$

2. 现在清楚了什么是更深层的Kolmogorov-Arnold表示：简单地堆叠更多的KAN层

现方案

1. 其中$n_i$是计算图中第$i$层节点的数量(比如当从0开始计数的话，上图第1层总计5个节点)
   且用 $(l,i)$ 表示第 $𝑙$ 层的第 $i$ 个神经元(比如上图$x_{1,2}$表示第1层第2个神经元)
   并用$x_{l,i}$表示$(l,i)$-神经元的激活值
   在第 $l$ 层和第 $l+1$ 层之间，有 $n_l{n}_{l+1}$ 激活函数(从第1层到第2层，$l=1$，则总计有5×1个激活函数)
2. 连接 $(l,i)$ 和 $(l+1,j)$ 的激活函数用下述公式表示(比如 ${\varphi }_{1,1,1}、{\varphi }_{1,2,1}、{\varphi }_{1,3,1}、{\varphi }_{1,4,1}、{\varphi }_{1,5,1}$)
   ${\varphi }_{l,j,i},l=0,\cdots ,L-1,i=1,\cdots ,n_l,j=1,\cdots ,n_{l+1}$
3. ${\varphi }_{l,j,i}$的预激活简单地是 $x_{l,i}$，即$x_{1,1}、x1,2、x1,3、x1,4、x1,5$
   ${\varphi }_{l,j,i}$ 的后激活用 ${\tilde{x}}_{l,j,i}\equiv {\varphi }_{l,j,i}(x_{l,i})$ 表示，${\tilde{x}}_{1,1,1}、{\tilde{x}}_{1,2,1}、{\tilde{x}}_{1,3,1}、{\tilde{x}}_{1,4,1}、{\tilde{x}}_{1,5,1}$
   第 $(l+1,j)$ 神经元即 $x_{2,1}$的激活值简单地是所有传入后激活的总和(定义为公式2.5)
   $x_{l+1},j=\sum _{l_i=1}^n{\tilde{x}}_{l,j,i}=\sum _{l_{i=1}}^n{\varphi }_{l,j,i}(x_{l,i}),j=1,\cdots ,n_{l+1}$
4. 以矩阵形式表示，这可以写成(定义成公式2.6，注意，一列一列的竖着看)

其中，${\Phi }_l$是对应于第$l$层的函数矩阵(B-spline函数矩阵)，$x$为输入矩阵

1. 一般的KAN网络是由 L𝐿层组成的：给定一个输入向量 $x_0\in {\mathbb{R}}^{n_0}$，KAN的输出是(定义为公式2.7)
   $KAN(x)=({\mathrm{\Phi }}_{L-1}\circ {\mathrm{\Phi }}_{L-2}\circ \cdots \circ {\mathrm{\Phi }}_1\circ {\mathrm{\Phi }}_0)x$

   最简的KAN则可以写为：$f(x)={\mathrm{\Phi }}_{out}\circ {\mathrm{\Phi }}_{in}\circ x$

2. 还可以重写上述方程，使其更类似于方程2.1，假设输出维度 $n$为1，并定义$f(x)\equiv KAN(x)$
   $f(x)=\sum _{i_{L-1}=1}^{n_{L-1}}{\varphi }_{L-1,i_L,i_{L-1}}(\sum _{i_{L-2}=1}^{n_{L-2}}\cdots (\sum _{i_2=1}^{n_2}{\varphi }_{2,i_3,i_2}(\sum _{i_1=1}^{n_1}{\varphi }_{1,i_2,i_1}(\sum _{i_0=1}^{n_0}{\varphi }_{0,i_1,i_0}(x_{i0}))))\cdots )$

异同

类似的，MLP也可以扩展到比较深、宽，比如写成仿射变换 W和非线性 σ的交错

$MLP(x)=(W_{L-1}\circ \sigma \circ W_{L-2}\circ \sigma \circ \cdots \circ W_1\circ \sigma \circ W_0)x$

很明显，MLPs将线性变换和非线性分开处理，分别表示为 W和 σ，而KANs将它们全部合
并在 $\mathrm{\Phi }$ 中。如下图(c)和(d)所示，便是一个一个三层MLP和一个三层KAN

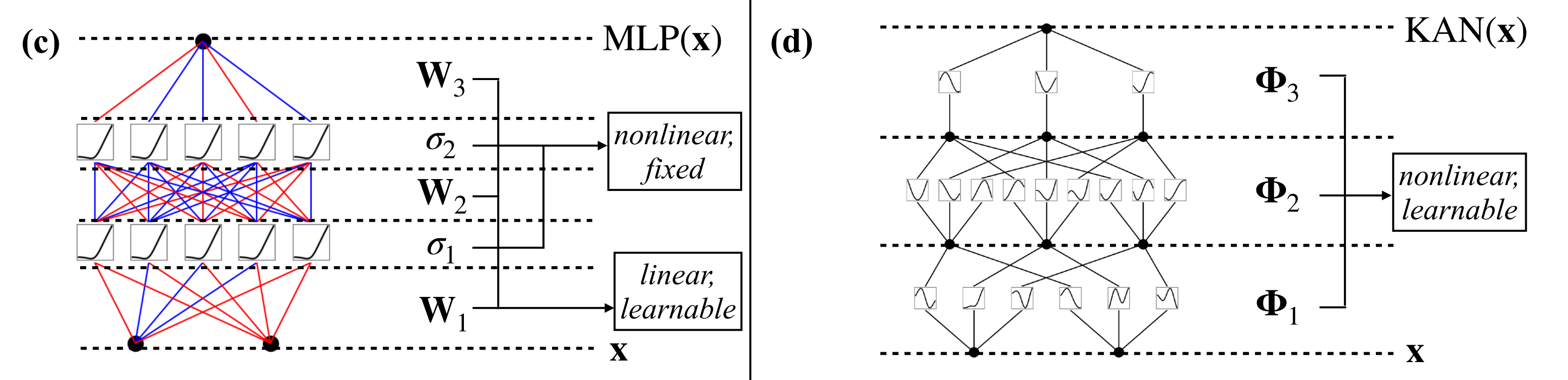
总结一下

• 与MLPs类似，KANs具有全连接结构
• 然而，MLPs在节点——「神经元」上具有固定的激活函数，而KANs在边——「权重」上具有可学习的激活函数，如下图所示
  

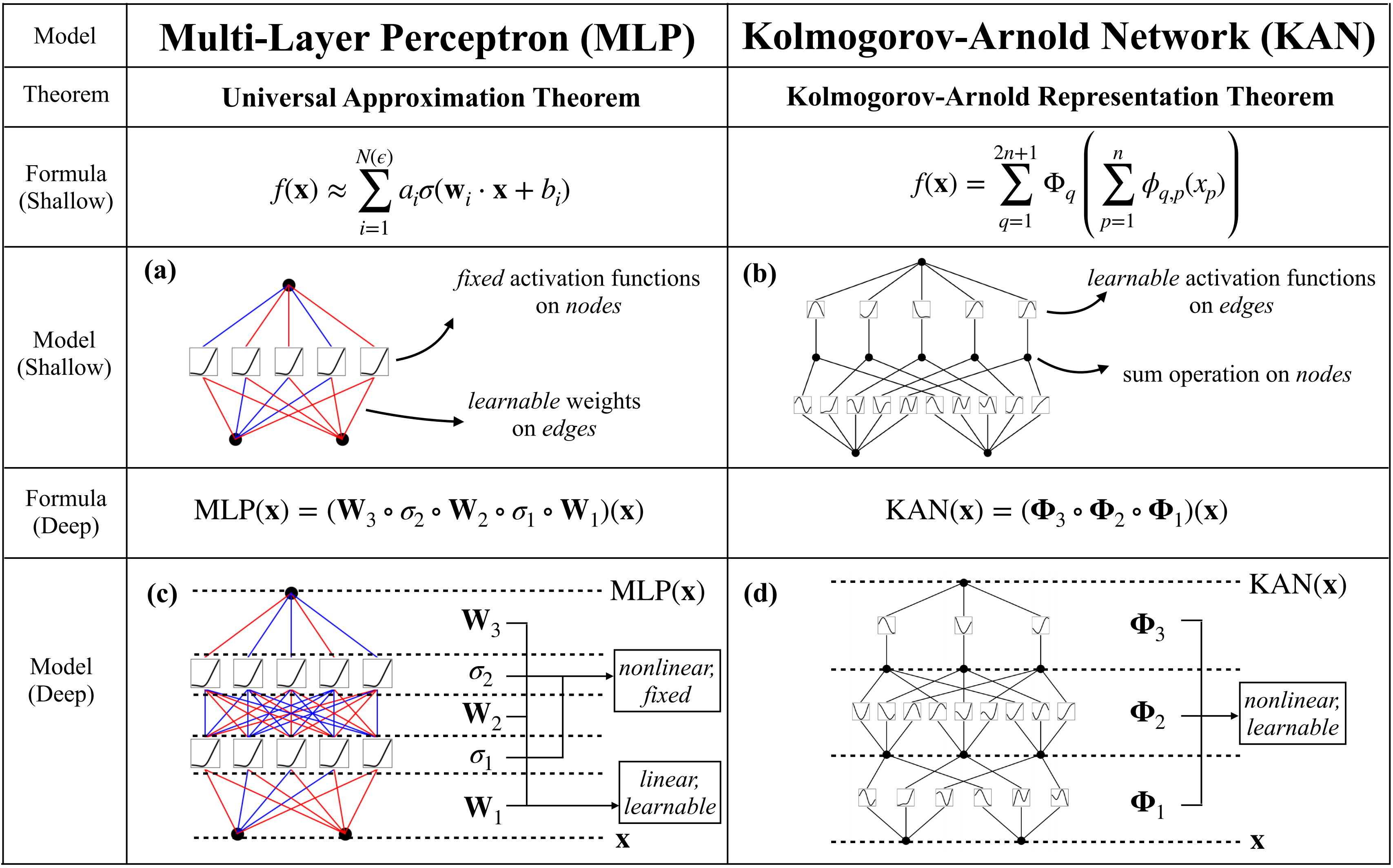
因此，KANs根本没有线性权重矩阵：相反，每个权重参数都被可学习的一维函数取代，参数化为样条函数
且KANs的节点只是简单地对传入信号求和，而不施加任何非线性