QTransformer

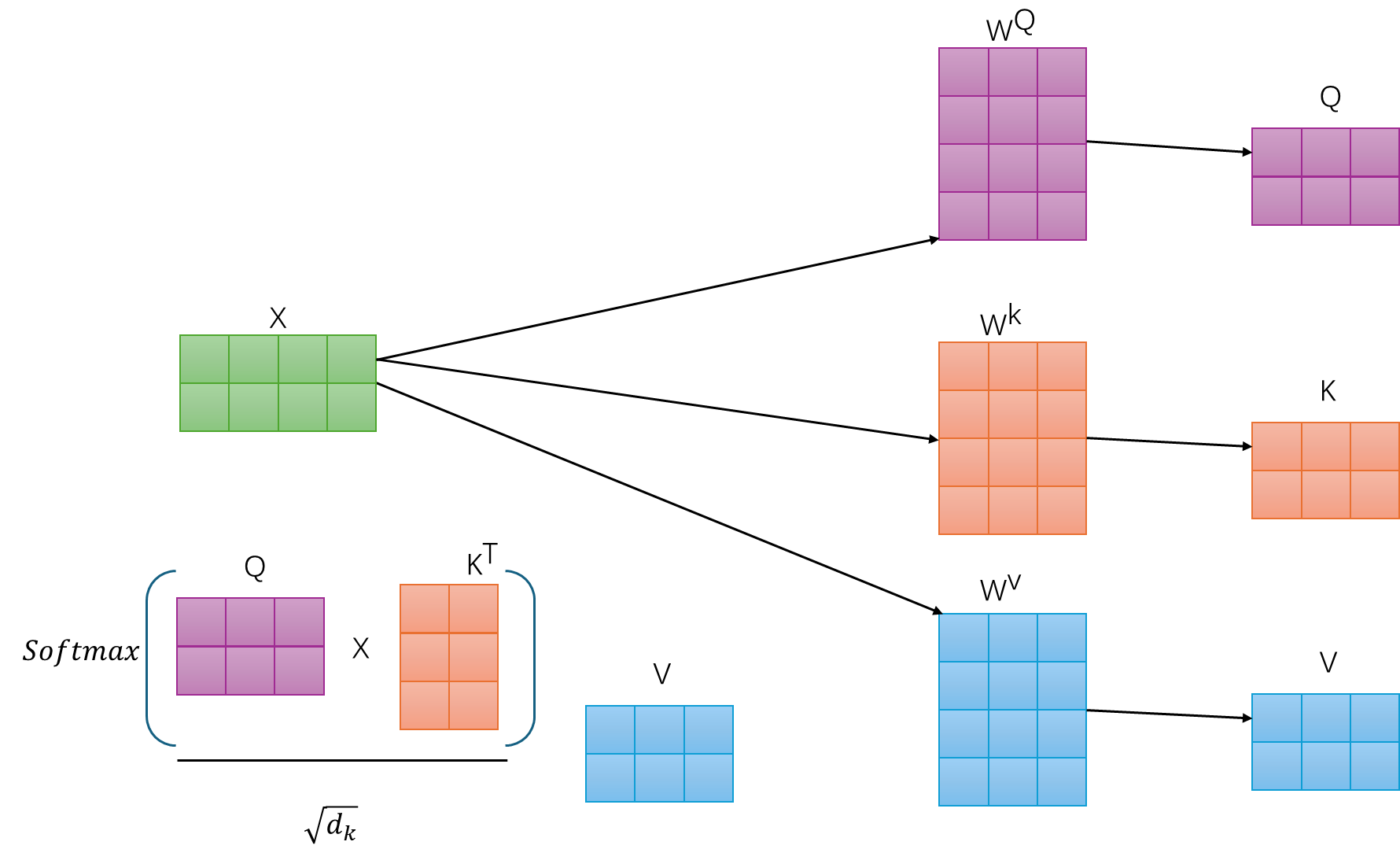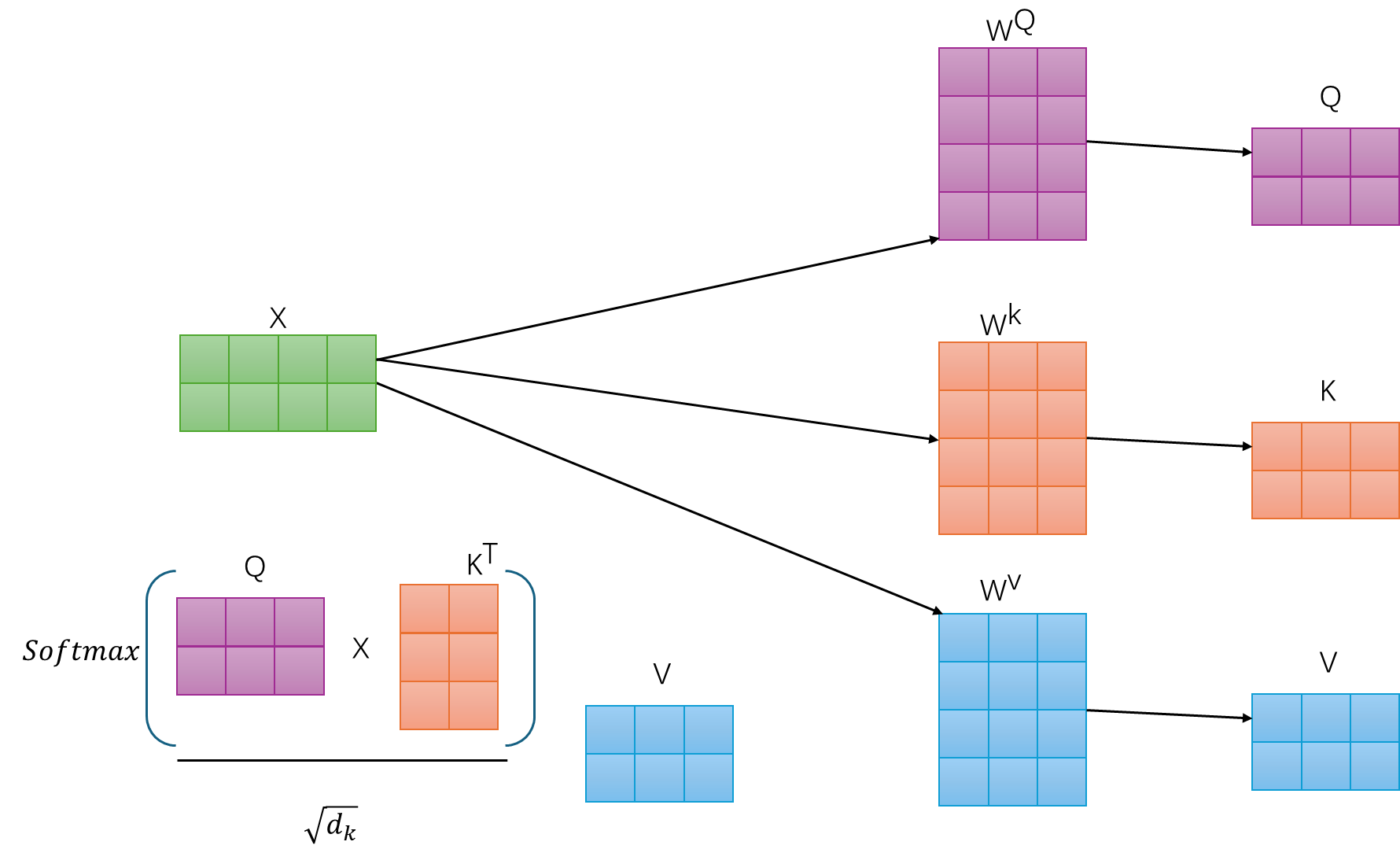
4*5 N*d
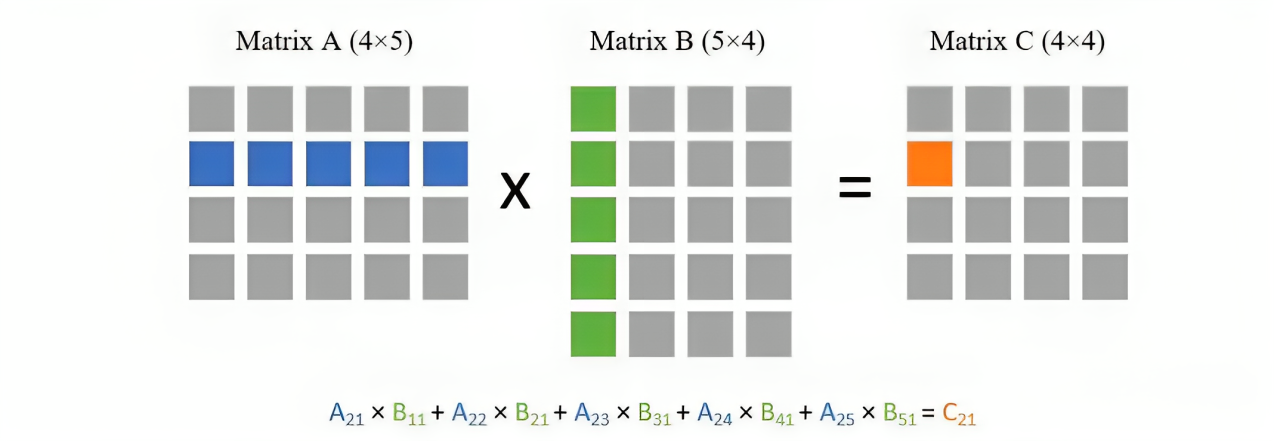
因为我们需要拿第一个矩阵的每一行去与第二个矩阵的每一列做点乘，所以总共就需要 $O(N^2)$ 次点乘。而每次点乘又需要 $d$ 次乘法，所以总复杂度就为 $O(N^{2}d)$

精确理解的话，当输入批次大小为 $b$，序列长度为 $N$ ​ 时，$l$ ​ 层transformer模型的计算量为 $l\ast (24bN{d}^2+4b{N}^{2}d)$  ​，$d$ ​则代表词向量的维度或者隐藏层的维度(隐藏层维度通常等于词向量维度)

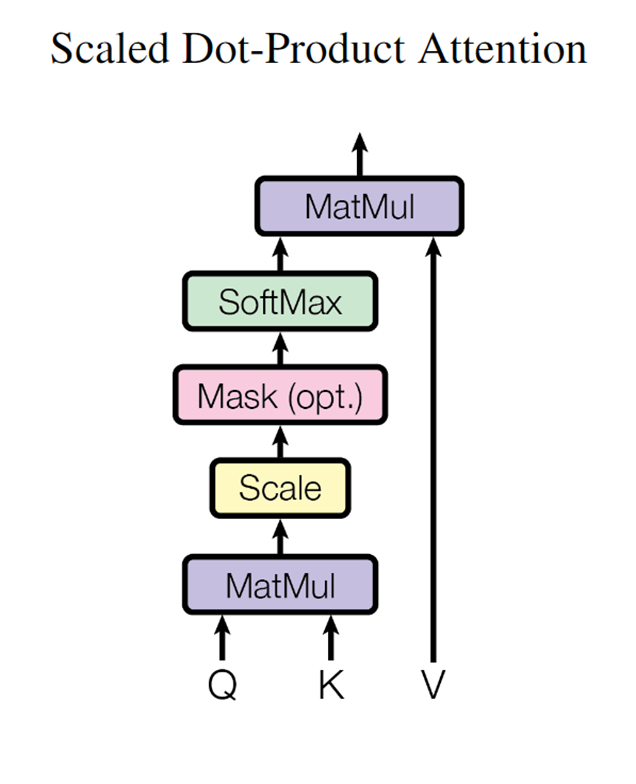
Self-Attention层的计算复杂度

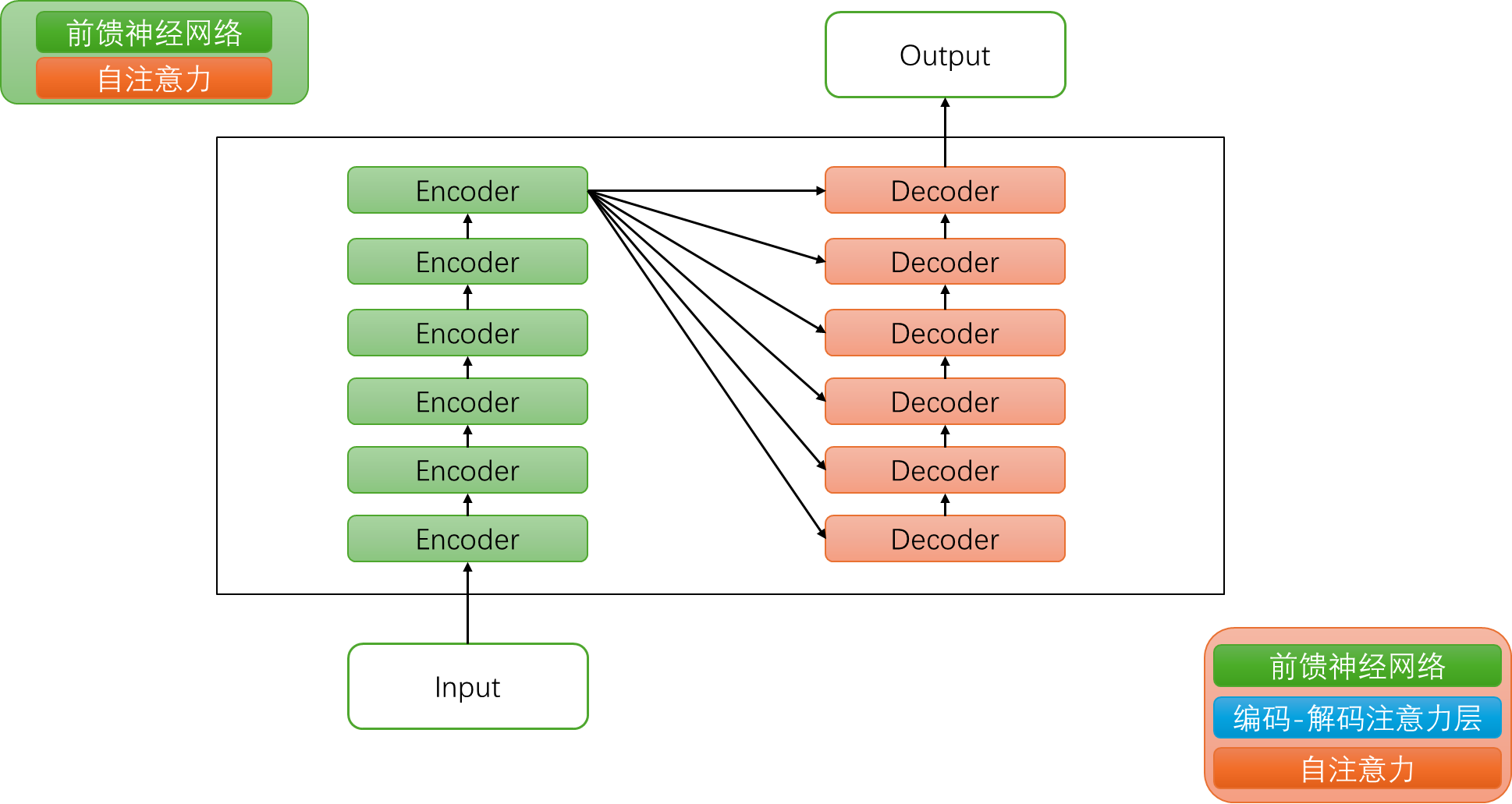
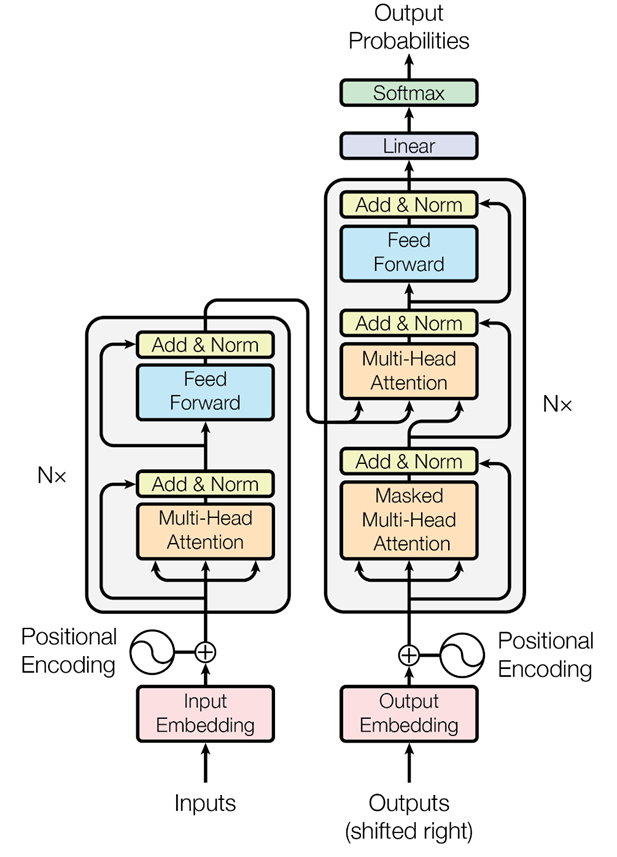
首先，我们知道，transformer模型由 $l$ 个相同的层组成，每个层分为两部分：self-attention块和MLP块

而self-attention层的模型参数有两部分，一部分是 $Q$，$K$，$V$ 的权重矩阵 $W_Q$、$W_K$、$W_V$ 和偏置，另一部分是输出权重矩阵 $W_O$ ​和偏置，最终为：$8bN{d}^2+4b{N}^{2}d$

具体怎么计算得来的呢？

1. 第一步是计算 $Q$ ​、$K$ ​、$V$
   即 $Q=x{W}_Q,K=x{W}_K,V=x{W}_V$
   该矩阵乘法的输入和输出形状为 $[b,N,d]\times [d,d]\to [b,N,d]$
   计算量为：$3\ast 2bN{d}^2=6bN{d}^2$
   (b,N,d)看做b个(N,d)，(b,N,d) × (d,d)看做b个(N,d) × (d,d)，(N,d) × (d,d)的计算次数是2Ndd(乘法Ndd、加法再Ndd，当然也有的资料不看加法
2. 计算 $Q{K}^T$
   该部分的输入和输出形状为
   $[b,head\mathrm{\_}num,N,per\mathrm{\_}head\mathrm{\_}hidden\mathrm{\_}size]\times [b,head\mathrm{\_}num,per\mathrm{\_}head\mathrm{\_}hidden\mathrm{\_}size,N]\to [b,head\mathrm{\_}num,N,N]$
   计算量为：$2b{N}^{2}d$ ​
3. 计算在 $V$ ​上的加权 $score\cdot V$
   该部分矩阵乘法的输入和输出形状为
   $[b,head\mathrm{\_}num,N,N]\times [b,head\mathrm{\_}num,N,per\mathrm{\_}head\mathrm{\_}hidden\mathrm{\_}size]\to [b,head\mathrm{\_}num,N,per\mathrm{\_}head\mathrm{\_}hidden\mathrm{\_}size]$
   计算量为：$2b{N}^{2}d$ ​
4. attention后的线性映射，矩阵乘法的输入和输出形状为 $[b,N,d]\times [d,d]\to [b,N,d]$
   计算量为 $2bN{d}^2$ ​
   最终自注意力层的输出结果为

$$x_{out}=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d}}\right)\cdot V\cdot W_o+x$$

MLP层的计算复杂度

MLP块由2个线性层组成，最终是 $16bN{d}^2$

怎么计算得来的呢？

一般地，第一个线性层是将维度从$d$映射到$4d$，第二个线性层再将维度从$4d$映射到$d$

$$x=f_{\text{gelu }}\left(x_{\text{out }}{W}_1\right)W_2+x_{\text{out }}$$

1. 第一个线性层的权重矩阵 $W_1$的形状为 $[d,4d]$，相当于先将维度从 $d$ 映射到$4d$​，矩阵乘法的输入和输出形状为$[b,N,d]\times [d,4d]\to [b,N,4d]$​，计算量为 $8bN{d}^2$
2. 第二个线性层的权重矩阵 $W_2$ 的形状为 $[4d,d]$，相当于再将维度从 $4d$​映射到 $d$，矩阵乘法的输入和输出形状为$[b,N,4d]\times [4d,d]\to [b,N,d]$，计算量为 $8bN{d}^2$

将上述所有表粗所示的计算量相加，得到每个transformer层的计算量大约为 $24bN{d}^2+4b{N}^{2}d$

logits的计算量：$2bNdV$

此外，另一个计算量的大头是logits的计算(毕竟词嵌入矩阵的参数量也较多)，将隐藏向量映射为词表大小，说白了，词向量维度通常等于隐藏层维度$h$ ，词嵌入矩阵的参数量为$Vh$​，最后的输出层的权重矩阵通常与词嵌入矩阵是参数共享的「解释一下，如七月杜老师所说，这个是transformer中一个重要的点，参数共享可以减小参数量，词嵌入矩阵是[vocab_size，hidden_size]，输出层矩阵是 [hidden_size，vocab_size]，是可以共享的」
其矩阵乘法的输入和输出形状为$[b,N,d]\times [d,V]\to [b,N,V]$，计算量为 $2bNdV$

因此，对于一个 $l$​ 层的transformer模型，输入数据形状为$[b,N]$​的情况下，一次训练迭代的计算量为上述三个部分的综合，即：